“Ant Colony Optimization”: Lessons in Transit Network Design from Ants

American Public Transportation Sucks.

Don’t worry, it’s not just you. For most Americans, public transportation is either inconvenient or entirely inaccessible. According to surveys conducted by the Department of Transportation, only 2% of Americans use public transit on their daily commute compared to an average of 10-20% in Western Europe. Additionally, a whopping 45% of Americans lack access to public transportation entirely [1]. 

As an integral component of the Engineering Grand Challenge to “Restore and Improve Urban Infrastructure,” finding a solution to efficient public transportation is far from easy. When designing transportation networks for major cities, planners face the impossible task of distilling a disorganized, complex, and ever-changing network of locations into an organized grid of routes and stops. To simplify this process, urban planning experts have historically relied on a set of models: namely, multi-hub networks, grid networks, and radial networks. These models are helpful in that each has a clear advantage over the others, providing planners with a certain level of flexibility when designing for a city’s particular needs. For instance, the centralized nature of radial network design is much better for cities with a vital downtown, whereas grid networks prioritize equal access across a wider area [2]. However, these models are otherwise rigid. They fail to take into account the changing needs of an expanding or retracting city. Additionally, they assume that expansion can take place in every direction, which is not the case for coastal cities in which 40% of the American population lives [3]. They are not incremental, either—they provide no “in-between” solution between the current state and the optimal state. 

Because of these shortcomings, modern urban planners no longer rely on these models. Instead, they look to something much more unconventional: ants, or more specifically, Ant Colony Optimization. By taking inspiration from the collaborative behavior of ants, the Ant Colony Optimization algorithm addresses many of the problems found in the aforementioned models. It not only provides an optimal transit network design, but also a systematic way of modifying existing designs. However, it does come with notable limitations.

 

A Background on Ant Colony Optimization

Much to my parents’ dismay, I loved ant farms in my youth. I enjoyed caring for them and feeling responsible for their well-being, but most importantly, I found their collaborative behavior fascinating. Somehow, without using language or any other form of nonverbal communication, each ant would know what the others around it were trying to accomplish. In his 1982 book titled Termitologia, French zoologist Pierre-Paul Grassé made a similar observation. He coined the term “stigmergy” to describe this strange phenomenon, defining it as the nature in which “the individual labour of each construction worker stimulates and guides the work of its neighbour” via pheromones [4].

During the years following Termitologia’s publication, ecologists and zoologists worldwide expanded upon Grassé’s findings through many studies about the collective behavior of ants. In 1988, researchers at Stanford suggested the notion of self-organization, implying that stigmergy allows ants to optimize productivity [5]. A 1989 study of Argentine ants extended this claim, asserting that ants use stigmergy to find optimal paths from one location to another [6]. Simultaneously, computer scientists began to observe similarities between stigmergy and the newly burgeoning field of artificial intelligence. Eventually, in 2006, Marco Dorigo and Thomas Stützle of the Université Libre de Bruxelles introduced their Ant Colony Optimization algorithm in “Ant Colony Optimization – Artificial Ants as a Computational Intelligence Technique” [7]. This publication was the first to successfully integrate stigmergy with artificial intelligence to effectively model complex, multi-agent systems.

How does Ant Colony Optimization work?

To understand the inner workings of the Ant Colony Optimization (ACO) algorithm, consider the following analogy. As pictured in Figure 1, imagine that you are standing at a trailhead and about to embark on a hike after a heavy winter storm. You must reach the top of the mountain to complete the hike, but the snow obscures the intended trail. With limited knowledge, you will likely take a somewhat random path based on your calculated but random “best judgment.” Some of your choices will be efficient, leading you closer to the top of the mountain while others will be inefficient. 

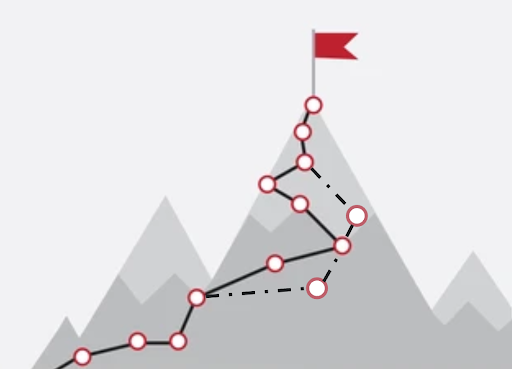
Figure 1. Two Possible Paths Up A Mountain. Different hikers will likely choose similar but distinct paths [8]. 

 

Figure 1 demonstrates a potential outcome when the next person hikes the same trail. They will have the same information available to you (in particular, the start and end points) but also have your footsteps to follow. Naturally, they will likely take the same path as you in most cases. Nonetheless, their “best judgment” might differ from yours, sometimes causing them to stray slightly or significantly from your original path. 

The ACO algorithm works under similar logic. Just as the input to our hiking analogy is a series of trailheads connected by a series of undiscovered trails, the input to ACO is a series of “nodes” connected by a series of “edges” (known in computer science as a graph). Likewise, the expected outputs of both our hiking analogy and ACO are the shortest—or “best”—path from the starting point to the destination. To produce this output, ACO performs three primary steps, repeated infinitely until a satisfactory result is achieved: (1) generate solutions, (2) compare solutions, and (3) update pheromones [9]. 

 

1. Generate solutions

During the initial step, ACO places a collection of agents (hikers, ants, etc.) into the graph at a predesignated source node. All agents have the same randomized destination node and are tasked with finding a path from the source node to the destination node. Just as each hiker makes random yet intentional choices to reach the top of the mountain in the hiking analogy, each ACO agent makes random but deliberate choices to reach the destination node. The aggregate of all of these choices is a unique path for each agent, referred to as their “solution.” It is important to note that ACO often releases many agents into the graph simultaneously, rather than one at a time. This approach distinguishes ACO from our hiking analogy, where only one agent explores the mountain at a time. 

2. Synthesize solutions

This logical step simply gathers the solutions of each agent so that they can be analyzed collectively. This does not have a direct equivalent in the hiking analogy, but it can be considered a “surveyor” that follows all of the paths made by previous hikers and records them in a notebook. 

3. Update pheromones

This step is the core mechanism of ACO and is inspired by the stigmergic behavior of ants observed by Grassé. In ACO, stigmergy is modeled with a mechanism called “pheromones,” which agents use to make decisions between alternate paths. Just as hikers leave footprints for others to follow, ACO agents leave “pheromones” on each path they traverse, which increases the probability that subsequent agents will choose their path. Pheromones also “evaporate” over time if not enough agents use a certain path, in the same way that a hiking trail may be “snowed over” if it is not frequently used. This process accelerates the rate at which the shortest paths become preferred.

 

After executing all three steps, ACO restarts at the first step, incorporating the changes from the previous iteration. As a result, the agents now begin at the destination node rather than the source node (in our analogy, they descend from the “top of the mountain” to the trailhead). Additionally, some paths will have pheromones remaining from the previous iteration, so agents no longer explore an empty graph. These steps are repeated many times, producing an output resembling Figure 2 below. \

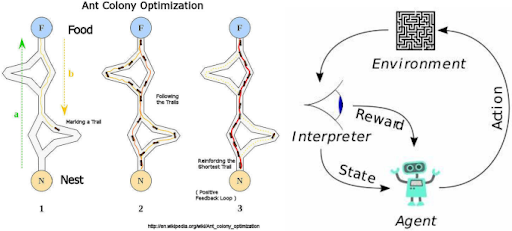
Figure 2. Possible Output of the Ant Colony Optimization Algorithm. Shorter paths allow agents to make more trips between the source node (N) and destination node (F), reinforcing that path until it is chosen by all agents [10].

 

As highlighted in Figure 2, the agents that choose the most efficient paths can make more trips between the source and destination nodes, causing more pheromones to accumulate on those trails. This creates a “positive feedback loop,” where the increase in pheromones attracts more ants, who, in turn, leave additional pheromones. Ultimately, this process leads to a single solution: the optimal (or near-optimal) path between the source and destination nodes. 

Applying ACO to Transit Network Design

ACO has existed in theory since Dorigo and Stützle’s publication in 2006, but it struggled to find relevant applications until recently. This is because the base algorithm described above only provides one use case—finding the shortest path from one starting point to one destination—a task more efficiently handled by algorithms like Dijkstra’s and A* [11]. Additionally, in applications like transit network design, a solution with only one path is not useful for making a network of connections between many locations. Rather, the magic of ACO lies in the many variations and extensions developed afterward. 

One such variation is detailed in “Urban-rural bus path planning based on ant colony optimization algorithm,” an article published in 2020 by Juan Li and Bo Wei of the Guilin University of Technology. In this variation, agents do not all move between the same source and destination nodes. Instead, as pictured in Figure 3 below, they move between unique sets of nodes, weighted to reflect variations in population density across different regions. Li and Wei propose this is a more realistic model for cities than the original algorithm, since public transit users rarely start and end in a shared location. To prove their model’s efficacy, the researchers used this variation to generate a hypothetical bus route for the Erqi District of Zhengzhou City, China. They found that ACO produced a solution within 99.7% of the theoretical optimal solution, demonstrating that the algorithm shows significant promise in specialized cases of route planning for public transit [12].

Figure 3. ACO-Suggested Bus Route for the Erqi District of Zhengzhou City, China. The route is 99.7% similar to the optimal route [12]. 

 

However, Li and Wei’s study introduces another potential shortcoming. While ACO could produce an optimal solution successfully, the process of implementing such a solution would be impossible. Developing public transportation infrastructure is time-consuming, and prematurely discontinuing the old system isn’t feasible without providing a viable alternative for its users [13]. This necessitates a gradual transition, which a variation of ACO provides. In the standard algorithm, all edges are initialized with no pheromones. Researchers at Zhengzhou University suggest an alternative approach, where pheromones are artificially planted on particular edges before the algorithm is executed. The idea is that these pre-initialized edges can represent existing bus or metro lines. Accordingly, agents closely follow the high-pheromone preexisting network when the simulation begins. But occasionally, they discover shorter paths and produce a solution that slightly improves the previous one. In this way, ACO still produces an optimal solution, while keeping the original transit network design in mind. After running ACO with these conditions, the researchers produced a solution that reused over half of the existing stops, namely 78 existing stops out of 152. They found that by adding or removing nodes from the graph, ACO also guides the expansion or reduction of transit systems [14]. Their research proves ACO models are powerful tools for distilling complex problems into implementable solutions.

What’s Next?

ACO is not a perfect solution to transit design. It has notable limitations that hinder its widespread adoption by urban planners, and ongoing research is focused on developing innovative solutions to address these challenges. One key problem is that the solutions suggested by ACO are still impractical. Despite the advances made by the team at Zhengzhou University, the retention rate of 78 out of 152 existing stops is unsatisfactory for immediate implementation. Modern-day research tackles this problem by limiting the algorithm to make only small modifications at a time, but has only increased the retention rate by 1.61-53.82% [15]. Therefore, significant advances are necessary to ensure that the results of ACO are undeniably helpful for planners. 

Another concern with using ACO to solve urban planning issues is its inability to fully reflect the complex social, political, and economic factors of the city for which it is designed. In an article titled “The ethics of algorithms,” Brent Middlestadt describes how all algorithms inherently make simplifications to their environments, requiring their creators to “privilege some values or interests over others” [16]. Therefore, applying ACO in urban planning may inadvertently prioritize certain communities or groups, leading to biased or incomplete solutions.

To learn more about the Ant Colony Optimization algorithm, any journal article in the Works Cited section is a good starting point. ANTS, an annual conference dedicated to ACO and related fields like swarm intelligence, is also a valuable resource. You can visit the conference’s website at https://www.aco-metaheuristic.org/ for the most recent ACO-related journal articles. Additionally, for a more technical analysis of the base algorithm, a helpful tutorial is available at https://www.youtube.com/watch?v=u7bQomllcJw.

Works Cited

1.  “The High Cost of Transportation in the United States,” Institute for Transportation and Development Policy – Promoting sustainable and equitable transportation worldwide, Jan. 24, 2024. https://www.itdp.org/2024/01/24/high-cost-transportation-united-states/
2. “Transit Networks,” National Association of City Transportation Officials, Apr. 21, 2016. https://nacto.org/publication/transit-street-design-guide/transit-system-strategies/network-strategies/transit-networks/
3. “Economics and Demographics,” Noaa.gov, 2015. https://coast.noaa.gov/states/fast-facts/economics-and-demographics.html
4. Pierre-Paul Grassé, Termitologia. Masson, 1984.
5. Frans Moyson, B. Manderick, and U. Brussel., The Collective Behavior of Ants. Artificial Intelligence Laboratory, Vrije Universiteit Brussel, Brussels, 1988.
6. S. Goss, S. Aron, J. L. Deneubourg, and J. M. Pasteels, “Self-organized shortcuts in the Argentine ant,” Naturwissenschaften, vol. 76, no. 12, pp. 579–581, Dec. 1989, doi: https://doi.org/10.1007/bf00462870.
7. M. Dorigo, M. Birattari, and T. Stützle, “Ant Colony Optimization Artificial Ants as a Computational Intelligence Technique,” Nov. 2006.
8. shutterstock.com, Mountain Info Graph Image. Accessed: Feb. 15, 2024. [1844284459]. Available: https://www.shutterstock.com/search/mountain-info-graph
9. M. Dorigo and StützleT., Ant colony optimization / Ant colony optimization. Cambridge, Mass.: Mit Press, 2004.
10. Y. Liu, B. Cao, and H. Li, “Improving ant colony optimization algorithm with epsilon greedy and Levy flight,” Complex & Intelligent Systems, vol. 7, no. 4, pp. 1711–1722, Mar. 2020, doi: https://doi.org/10.1007/s40747-020-00138-3.
11. D. Foead, A. Ghifari, M. Budi Kusuma, N. Hanafiah, and E. Gunawan, “ScienceDirect-NC-ND license (https://creativecommons.org/licenses/by-nc-nd/4.0) Peer-review under responsibility of the scientific A Systematic Literature Review of A* Pathfinding-NC-ND license (https://creativecommons.org/licenses/by-nc-nd/4.0) Peer-review under responsibility of the scientific A Systematic Literature Review of A* Pathfinding,” Procedia Computer Science, vol. 179, pp. 507–514, 2021, doi: https://doi.org/10.1016/j.procs.2021.01.034.
12. J. Li and B. Wei, “URBAN-RURAL BUS PATH PLANNING BASED ON ANT COLONY OPTIMIZATION ALGORITHM,” The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, vol. XLII-3/W10, pp. 451–456, Feb. 2020, doi: https://doi.org/10.5194/isprs-archives-xlii-3-w10-451-2020.
13. J. R. Krogstad and M. D. Leiren, “Gradual change towards re-integration: Insights from local public transport in Norway,” Public Policy and Administration, vol. 31, no. 4, pp. 324–341, Aug. 2016, doi: https://doi.org/10.1177/0952076716634828.
14. Y. Jiang et al., “Citation,” International Journal of Geo-Information, 2022, doi: https://doi.org/10.3390/ijgi11050317.
15. B. Wu, X. Zuo, M. Zhou, X. Wan, X. Zhao, and S. Yang, “A Multi-Objective Ant Colony System-Based Approach to Transit Route Network Adjustment,” IEEE Transactions on Intelligent Transportation Systems, pp. 1–15, 2024, doi: https://doi.org/10.1109/tits.2023.3348111.
16. B. D. Mittelstadt, P. Allo, M. Taddeo, S. Wachter, and L. Floridi, “The ethics of algorithms: Mapping the debate,” Big Data & Society, vol. 3, no. 2, p. 205395171667967, Dec. 2016, doi: https://doi.org/10.1177/2053951716679679.