It’s the weekend after Black Friday. You spontaneously remember that you forgot to find a Christmas gift for your best friend. Inspiration strikes. Your friend is part of the record hobby revival trend. To be sure that your gift arrives on time, you scramble to your laptop, enter your credit card information, and order the quintessential Pink Floyd album, The Dark Side of the Moon. Mission accomplished. Who needs Santa when there is modern technology? But worry strikes. Given that your internet traffic can be seen by a number of eyes (e.g., your internet service provider, the government, or perhaps someone who has hacked your network), you realize that you are unwittingly putting a lot of trust in the security of your card information [11].
The revolution of modern cryptosystems like RSA (Rivest–Shamir–Adleman) affirms your trust. However, for many of us, these cryptosystems are…cryptic. When you enter sensitive personal information online, you can be sure it is secure, in essence, because it is difficult to find a large number’s prime factorization1 [12]. If that sounds daunting, do not worry. I will unpack it all. By understanding how RSA works, you will gain mathematical trust in your data’s security, and you need not worry about your online Christmas shopping.
There is a lot of beautiful, surprisingly practical math involved in securing our internet data: a task so essential to the function of modern society that we often take it for granted. Because of its popularity and relative simplicity, I choose to explain how RSA uses number theory (the study of integers) to secure our bank transactions, private messages, account authentication, and many more vital modern activities [11]. Along the way, we get to explore the basics of public-key-cryptography and the future of the ever-changing field, which includes the impending doom of quantum computers. Even if math is not your forte, I encourage you to open your mind to some things that I find fascinating. You may enjoy the learning process! And, when you enter your bank password next time, I hope you view it in an entirely new way, fully trusting that your data will be secure.
Some Number History
When some of the all-time number theory greats like Euclid (300 BC), Euler (18th C), Gauss (19th C), and Riemann (19th C) were finding the beautiful organization of the structure of the integers (i.e., …, -3, -2, -1, 0, 1, 2, 3, …), I posit that they saw no future in its applicability. Perhaps, however, one unsuspecting English economist, William Stanley Jevons, got a glimpse of the future, asking “Can the reader say what two numbers multiplied together will produce the number 8616460799? I think it unlikely that anyone but myself will ever know2 [7].”Indeed, this observation is essential to RSA. Even still, I doubt that Jevons saw how this interesting property of numbers,or more accurately, our inability to make sense of them, can lead to a revolution in public key cryptography.
History has seen many forms of cryptography before the modern era. For example, the Caesar Cipher was used by Julius Caesar himself in private correspondence [2]. This works by shifting each letter in a message over by a certain number of positions in the alphabet. For example, I can shift each letter to the right by five to create this translation palate (with normal letters on the top row translating to the cipher text on the bottom row):
| A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
| F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C | D | E |
With Caesar’s Cipher, “THIS PAPER IS ABOUT RSA” turns into “YMNX UFUJW NX FGTZY WXF.” Of course, the pattern here is relatively easy to decipher, and modern encryption must be far more clever given the power of computers in cracking algorithms.
Public Key Cryptography
For some reason, Alice and Bob are used canonically when describing how public-key cryptography works. I have no good reason not to follow this convention. Imagine Alice wants to send a private message to Bob. In public-key-cryptography, which is used for RSA and other cryptographic internet systems, Bob generates two keys: one public and one private. Everyone can see the public key. Everyone can encrypt a message using the public key. Alice does this. The result is a stream of numbers and letters called a hash that no one can make sense of. Well, no one except Bob. If the key generation is performed in a secure way, then it is nearly impossible to figure out Bob’s private key. Alice can sleep happily knowing that no one laid eyes on her messages [3]. In practical implementation, you can imagine how a system like this is useful for sending digital signatures, emails, files, or any number of other digital information formats.
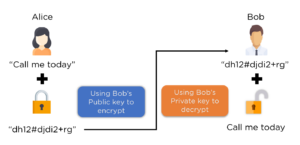
Schematic of a Public Key Cryptosystem [14]
From an engineering perspective, how does this actually work? What kind of system would be effective in creating undecipherable hashes that secure your data? In the case of RSA, number theory comes to the rescue in generating public and private keys. Before seeing exactly how it does this, we must learn a bit of number theory.
Some Light Number Theory
Before you get scared, know that you did this stuff in grade school. I suspect most readers know what a prime number is, for example. If not, do not worry, I will explain it all. Even better, you have the luxury of not dredging through all the proofs involved. I took a course in number theory. You can trust me with these results. Firstly, a definition: a prime number is a number that is only divisible by 1 and itself. 2, 3, 5, 7, 101, 7919, and 282,589,933 – 1 are all prime. 2 is the only even prime. Do you see why? The last prime I mentioned is the largest known prime, at least to our species. As numbers get quite large, one might expect that there exists a cutoff point where all subsequent numbers are divisible by something. But no: Euclid found that there are an infinite number of primes. There is always a next prime.
Primes are important in the context of RSA because of a number’s prime factorization, which is its representation as a product of primes. For example, 6 = 2 x 3 is its prime factorization. The important Fundamental Theorem of Arithmetic states that every number has a unique prime factorization3.
12 = 22 x 3.
7 = well, 7
1000 = 23 x 53
This, hopefully, seems intuitively true, and it is essential for RSA.
Just one more tool is needed to understand RSA: congruence. We say “x is congruent to y modulo n” if x – y is divisible by n. This notation is: x≡y (mod n). Some quick examples are:
6≡3 (mod 3) since 6 – 3 is divisible by 3.
21≡1 (mod 5) since 21 – 1 is divisible by 5.
50≡-50 (mod 100).
-50≡50 (mod 100) and so on.
Note that there is a periodic nature to addition modulo n. Specifically, as x increases, y will get back to where it started. A clock, for example, uses addition modulo 12. At noon if another hour passes, 12+1≡1 (mod 12), so it is now one o’clock.
For full connection, the Caesar Cipher can be described concisely with the tool of modular arithmetic. Let 0 correspond to A, 1 to B, 2 to C, etc. Let x be a letter in the original message and y the encrypted letter. Then, y≡x+5 (mod 25) since there are 26 letters in the alphabet.
How RSA Works
Now, we are ready to make sense of RSA, which is the modern form of encryption that keeps your personal information safe, even from computer attacks. To keep things grounded, let’s say Alice is entering her bank password “I_Like_Dogs_47” to gain access to her account at Bob Bank. Here is the process Bob Bank uses to generate a private/public key pair [3].
- Bob Bank chooses two random large primes: p and q. Bob Bank computes N=p*q.
- Next, Bob Bank computes N=p-1*(q-1)4.
- Bob Bank chooses a number e less than N such that e is relatively prime to N. That is, the greatest common divisor of N and e is 1 (e.g., 34 and 15 are relatively prime since their greatest common divisor is 1).
- Bob Bank finds a number d such that d*e ≡1 (mod φ(N)).
Done! Bob Bank’s public key consists of N and e, while its private key consists of d. All these steps mentioned can be performed with computational ease, even though real-life secure RSA implementations calculate N values with 600+ decimal digits5!These numbers may seem arbitrary, but they will enable Bob Bank to decrypt any message or password that comes its way.
Now, Alice wants to enter her password, “I_Like_Dogs_47” for account access. To your computer, everything is a number, so Alice first converts her password into a number, M. There are a variety of ways to do this in practice. To send it to Bob Bank:
- Alice computes the ciphertext C≡Me (mod N). Remember, e and N are part of Bob Bank’s public key, so Alice has access to them. The ciphertext is a new number that I earlier called a hash. Any outside observer can see C, but they cannot make sense of it since Alice encrypted it.
- Bob Bank receives C and computes Cd≡M (mod N) to decrypt Alice’s password. That M is the same password Alice sent, so Bob Bank now knows that the user on the other side is, indeed, Alice. Nobody else could imitate Alice since, in principle, no one besides Bob Bank has access to d. In other words, an observer could never convert the hash into a meaningful password.
Why is This So Effective?
The main idea of RSA is that given M, N, and e, it is incredibly difficult to find d [3]. If RSA is implemented in “smart” ways that prevent common types of attacks, the main strategy to decrypt the message M is to find the prime factors of N. Remember, by the Fundamental Theorem of Arithmetic, there is only one pair of factors p and q. What are these common attacks? Well, RSA is old, having been invented in 1977. Instead of describing all the defenses to possible RSA attacks, I will rely on Stanford cryptography expert Dan Boneh:
Two decades of research into inverting the RSA function produced some insightful attacks, but no devastating attack has ever been found. The attacks discovered so far mainly illustrate the pitfalls to be avoided when implementing RSA. At the moment it appears that proper implementations can be trusted to provide security in the digital world. [3]
Assuming good implementation, hackers are left to the strategy of factoring N. As it turns out, factoring N into p and q allows for easy computation of d, and thus also M [3]. However, no efficient algorithm exists for finding the prime factorization of large integers [12]. If I choose p and q to be 43 and 47, then it is not hard to find them from N = 2021. But a real-life RSA key looks more like…
N =
23383677215583959359033322449312532881778545134917552020025754123608293086486673247362177595757591513513785849971756217078078674708818353464185545598509078759165649996596464580787344804595100246543849628155661960173840229517600655555429471357410699769785880409561604214554198402296337524815492174004007914348515759133017385036517396581165807051749477751166074724956100139987957571227050586865449327297717731926699654806553536562713280121823993875270250289917439694596533761503739805522394136130076866359303567318898460957025887187943803189202206839811198198710842579809032585173961974779199602416283241059682741369141 [9]
Try factoring that! It should give you a sense of security in your own encryption. The number above is a 2048-bit key, and the largest RSA key factored to date has 829 bits (250 decimal places), which is tiny in comparison [10]. Also, this record factorization relied upon supercomputers and took 2700 core-years [10]. That is, a single CPU core would take 2700 years to perform the calculation. With factorization out of question, perhaps a hacker’s next best trick to gain access to your account is by brute-forcing your password. This would be too computationally challenging. This famous chart sums up the improbability of brute-forcing passwords:

Difficulty of Brute-Forcing Passwords [1]
Given the security of RSA, brute-forcing a password may seem viable, but my point is that you, the user, can prevent this alternative from being realistic by choosing strong passwords. For example, the password “R*S*A_4096#Sobo” would take, in theory, a billion years to decrypt. You choose a long password with variation. You use properly implemented RSA using 2048+ bit keys. What could possibly create a security vulnerability? Shockingly, the answer brings us to quantum computing and more advanced algorithms.
Quantum computers have been discussed for a long time, and while they are not yet practical or dynamic, they are more real than most people realize. Companies like IBM and Google perform research using real quantum computers that execute real algorithms [15]. Quantum computers utilize quantum mechanics in their operation to execute certain algorithms exponentially faster than a classical computer [5]. The key here is that there is no improvement if there is no quantum algorithm. Indeed, a huge roadblock in the field is actually finding these algorithms, which is much harder than developing classical algorithms (i.e., algorithms that would work on the computer you are using) [5]. However, breakthroughs have been made. As you may have expected by now, there are quantum algorithms that could break RSA. In 1995, Peter Shor made a revolutionary discovery by finding a quantum algorithm that finds a number’s prime factorization [13]. It is known as Shor’s Algorithm. Remember: the critical private key value d can be found if one can find the prime factorization of N. The implication of Shor’s Algorithm is that, if run on a large enough quantum computer, it would be able to factor N almost instantaneously. Thus, it would break RSA. If this algorithm were scalable to crack large RSA keys, then it would ruin internet security if used bythe wrong hands.

One of IBM’s Quantum Computers [14]
Quantum computers exist. Shor’s algorithm exists. So, do you have to worry about your security? No. The largest integer factored using Shor’s algorithm in practice is a laughable 21 = 7 x 3 [6]. Clearly, these computers have a long way to go. This leaves us wondering: what happens when quantum computers do become scalable? Indeed, it would be paradigm-shifting. RSA would be obsolete. This possibility has opened a new dichotomy in cryptography: pre vs post quantum cryptography. Researchers have identified various post-quantum cryptosystems that are thought to protect information against a quantum revolution. In other words, there is no (known) quantum algorithm that can break these cryptosystems [5]. These include lattice-based cryptography, secret-key cryptography, and the scary-sounding multivariate-quadratic-equations cryptography [5]. It is unfeasible to describe these systems in detail, but, as you may expect, they rely on very abstract mathematical ideas, many of which are far more advanced than those used in RSA. Since RSA can break due to a quantum revolution, it is merely pre-quantum.
To avoid being too optimistic, there is one threat on the horizon that should make us uneasy. Kevin Townsend, an information security expert describes how “Bad actors, especially nation state attackers, are stealing encrypted data now with the expectation of being able to decrypt in the future [8].” Our encrypted information, while secure, is being stockpiled. One day, when quantum computing becomes feasible, these “bad actors” could gain access to our data as part of a “harvest now, decrypt later” strategy. Of course, such a strategy is only a threat if quantum computers make a lot of progress, but some experts think that quantum computers may become sufficiently advanced for cyber-attacks within 20 years [8]. To be safe, companies should start preparing now with better technology, including post-quantum cryptosystems, to ensure future security. As internet users, all we can do is support enhanced security while using strong passwords. Likely, given the number of assumptions involved in the success of “harvest now, decrypt later” strategies, we have nothing to fear.
I have heard people question the security of information in the digital age, but I hope I have restored your faith in an important part of modern technology. Granted, there are some boxes to check. I mentioned that RSA must be implemented in a “smart” way to be fully secure. For engineers, do your due diligence and implement things the right way. For other internet users, it is worth researching the security of the systems you are using. Also, make sure to use good passwords! Assuming proper usage, the human race’s deep understanding of our technological limitations can assure you that your information will be hidden behind a number theoretic fog of abstraction, and only you can Illuminate it.
Works Cited
[1] C. Neskey, “Are your passwords in the green?,” Hive Systems, 30-Jan-2023. [Online]. Available: https://www.hivesystems.io/blog/are-your-passwords-in-the-green. [Accessed: 05-Mar-2023].
[2] “Caesar Cipher,” Brilliant Math & Science Wiki. [Online]. Available: https://brilliant.org/wiki/caesar-cipher/#:~:text=A%20Caesar%20cipher%20is%20a,an%20A%2C%20and%20so%20on. [Accessed: 05-Mar-2023].
[3] D. Boneh, “Twenty Years of Attacks on the RSA Cryptosystem,” Notices of the American Mathematical Society (AMS), vol. 46, no. 2, pp. 203–213, 1999.
[4] D. J. Bernstein and T. Lange, “Post-quantum cryptography,” Nature, vol. 549, no. 7671, pp. 188–194, 2017.
[5] D. J. Bernstein, “Introduction to post-quantum cryptography,” Post-Quantum Cryptography, pp. 1–14.
[6] E. Martín-López, A. Laing, T. Lawson, R. Alvarez, X.-Q. Zhou, and J. L. O’Brien, “Experimental realization of Shor’s quantum factoring algorithm using qubit recycling,” Nature Photonics, vol. 6, no. 11, pp. 773–776, 2012.
[7] “Jevons’ Number,” Wolfram MathWorld. [Online]. Available: https://mathworld.wolfram.com/JevonsNumber.html. [Accessed: 05-Mar-2023].
[8] K. Townsend, “Solving the quantum decryption ‘harvest now, decrypt later’ problem,” SecurityWeek, 16-Feb-2022. [Online]. Available: https://www.securityweek.com/solving-quantum-decryption-harvest-now-decrypt-later-problem/. [Accessed: 02-May-2023].
[9] Online RSA key generation. [Online]. Available: https://www.mobilefish.com/services/rsa_key_generation/rsa_key_generation.php. [Accessed: 05-Mar-2023].
[10] P. Zimmermann, “NMBRTHRY Archives,” North Dakota University System Listserv. [Online]. Available: https://listserv.nodak.edu/cgi-bin/wa.exe?A2=NMBRTHRY%3Bdc42ccd1.2002. [Accessed: 05-Mar-2023].
[11] “RSA cryptography: The Algorithm Keeping Us Safe Online,” National Inventors Hall of Fame. [Online]. Available: https://www.invent.org/blog/inventors/rsa-cryptography-algorithm#:~:text=At%20its%20core%2C%20RSA%20is,securing%20communication%20on%20the%20internet. [Accessed: 05-Mar-2023].
[12] “RSA encryption,” Brilliant Math & Science Wiki. [Online]. Available: https://brilliant.org/wiki/rsa-encryption/. [Accessed: 05-Mar-2023].
[13] “Shor’s algorithm,” IBM Quantum. [Online]. Available: https://quantum-computing.ibm.com/composer/docs/iqx/guide/shors-algorithm. [Accessed: 05-Mar-2023].
[14] “Symmetric vs. Asymmetric Encryption – What are differences?,” SSL2BUY. [Online]. Available: https://www.ssl2buy.com/wiki/symmetric-vs-asymmetric-encryption-what-are-differences. [Accessed: 05-Mar-2023].
[15] “Toyota and Mitsubishi Chemical to use IBM Quantum Computer,” Nikkei Asia, 29-Jun-2021. [Online]. Available: https://asia.nikkei.com/Business/Technology/Toyota-and-Mitsubishi-Chemical-to-use-IBM-quantum-computer. [Accessed: 05-Mar-2023].




